Learning the Exit (part 2)
As described in my prior post Learning the Exit (part 1), I have a model that indicates mean reversion entries with ~81% accuracy, however I did not have a good approach in handling the exit. While 81% of MR signals had a minimum profit of 25% (of prior amplitude), the mean profit available was 150%, pointing to a larger profit opportunity to be had if can better handle the exit.
I have found it very difficult to predict the magnitude of the optimal MR returns a-priori (at the point of entry) in these scenarios, achieving a \(r^2\) of only 20% with various regression models. Hence the approach calls for online decision making as to how to position and when to exit post entry.
We want to determine a policy function \(\pi_{\theta}(a | s_t)\) to indicate the appropriate action to taken for each bar post entry. In order to learn this function, be it with a genetic algorithm or reinforcement learning, we need to define an objective/reward function.
Objectives
The reward function should include the following objectives:
- reward for proceeding on a profitable path
- penalty for proceeding on an unprofitable path
- penalty for non-performance in a prolonged sideways move
- penalty for amount of risk assumed
- transaction costs + slippage
A reward approach
Many papers take the approach of deferring reward until position exit, i.e. rewarding \(r_t = 0\) from \(T_{entry}\) to \(T_{exit-1}\) while in position, and only presenting the cumulative reward at \(T_{exit-1}\). However, this approach leads to the credit assignment problem, where individual actions during the holding period have an unassigned reward, requiring the RL algorithm to approximate the implied reward through some form of backward induction.
We will avoid the credit assignment problem, and hopefully motivate a faster and more accurate convergence towards a policy model. Providing continuous reward also should make the problem more amenable to gradient descent approaches.
Making use of our Labeler, we can label the cumulative return from the start of the MR signaling \(T_{start}\) to some maximum \(T_{start} + \Delta T\). Using these labels can determine the extent of upward, downward, and sideways price (return) movements.
Take 1
For each “bar” we will assign a reward based on the direction of the labeled extents:
- for upward sloping return movements: reward = dr/dt x position
- note that dr/dt (slope) is positive, yielding a positive reward
- for downward sloping return movements: reward = dr/dt x position
- note that dr/dt (slope) is negative, yielding a negative reward
- for sideways movements: reward = 0
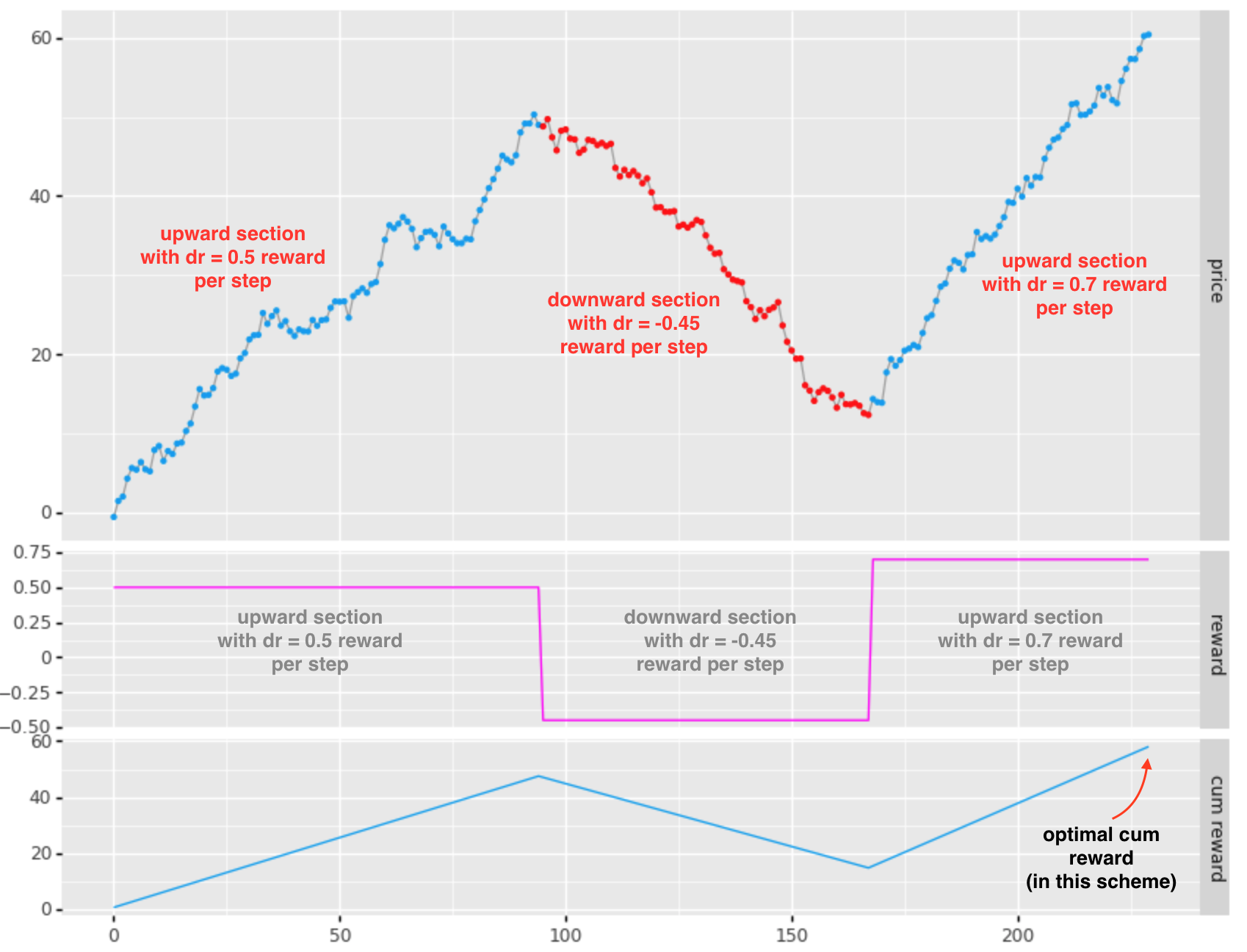
The cumulative reward in this scheme seems to be headed in the right direction, however takes considerable drawdown risk (-39 bps) in order to achieve an additional 10bps. I would like to see the optimum at the end of the 1st upward section (in this case).
Take 2
The prior reward system did not add extra penalty for drawdown. Without some additional penalty for drawdowns, the optimal reward will be achieved at an end point with the maximum return, regardless of unrealized drawdown. To ameliorate this we use the following scheme:
- for upward sloping return movements: reward = dr/dt x position
- as above
- for drawdowns: reward = drawdown penalty x dr/dt x position
- we add a penalty to discourage riding through drawdowns for minor eventual gains
- for sideways movements: reward = sideways penalty x position
- this acts as a discount factor, penalizing for non-performance during extended sideways moves
Using a penalty of 2.0x for downward moves, the reward and cumulative looks like:
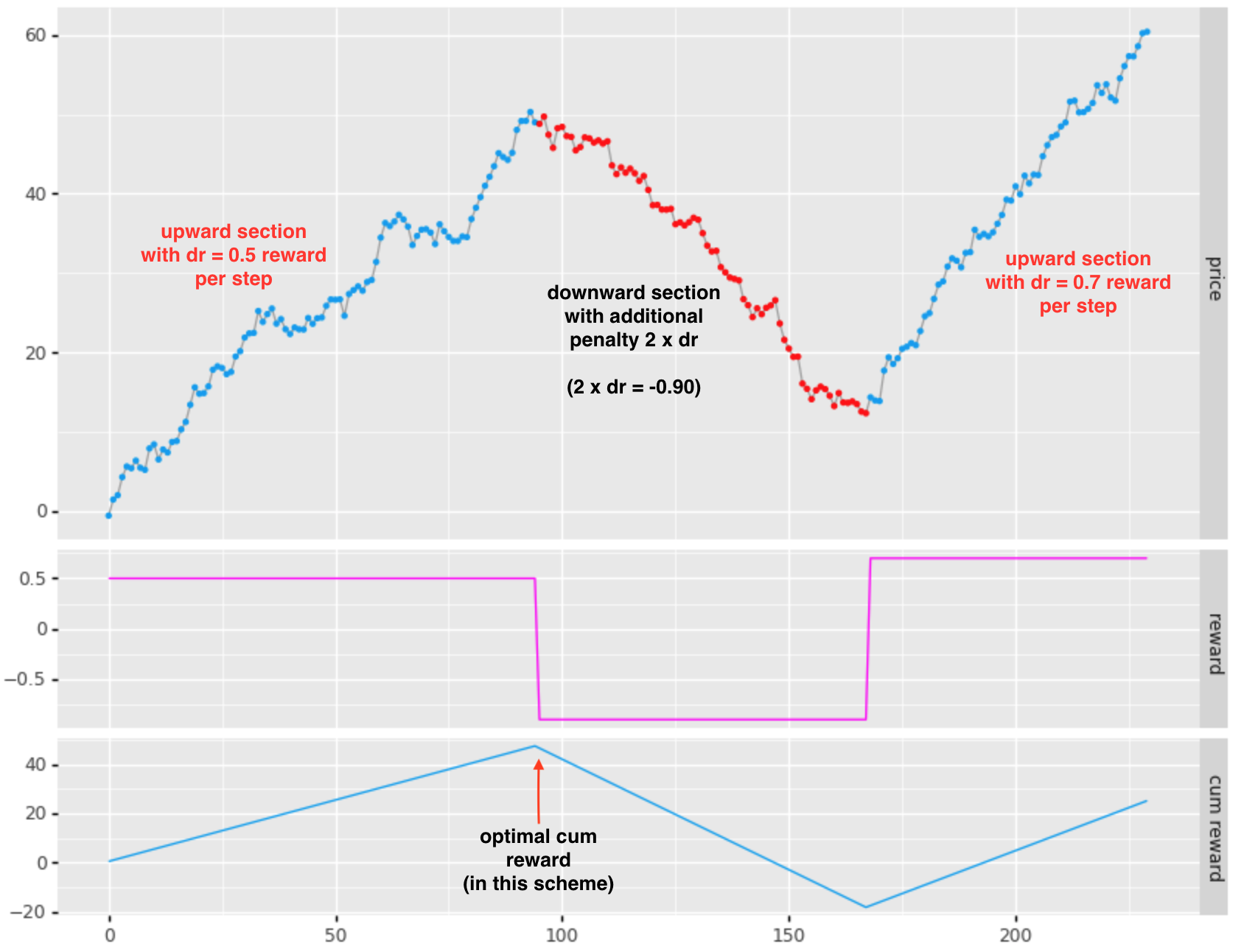
This is good, as now the optimum shows my preference for not riding through the -39bps of drawdown in order to achieve an additional 10bps above the 50bp move of the first section.
Taking this further
There are other aspects one may wish to incorporate into the reward function, for example:
- time:
- do we discount rewards as time proceeds further away from signal inception?
- transaction cost:
- do we incorporate transaction cost at the point of entry or do we spread the cost across the holding period? Allocating the transaction cost to the reward at entry would tend to present a negative reward on entry even when the entry is optimal (or likely to be profitable).
- we could potentially ammortize the transaction cost across the remaining direction. If the agent does not hold for the full extent of the direction, the remaining cost is allocated in the exit reward.
- we could also penalize for the amount of noise in a move, preferring less noisy moves.
Finally, would love to hear from readers regarding your own RL experience, problem setup, etc.