New Crypto Strategy

I have a new stat/arb strategy in crypto that uses an adaptive state based system to identify MR opportunities on small portfolios of coins. I have identified ~1600 such portfolios across 200 coins, each of which is traded as a strategy. In practice I trade a portfolio of these strategies (which I term, “stratlets”), where the strategy is defined as a dynamically weighted portfolio of these stratlets.

Setup

While each stratlet is adaptive, adjusting internal parameters over time, there are some hyper parameters for the following layers:

• model:
  • 5 dynamic parameters inferred over time
  • 1 fixed parameter
  • 1 parameter to be optimised
• trading state machine:
  • 3 parameters to be optimised
• money management:
  • 2 parameters to be optimised

In order to avoid overfitting, rather than optimising all 6 free parameters at once, took the following approach:

1. optimise each layer separately: i.e. the model, trading, and MM are optimised separately
2. restrict the parameter values to a small # of discrete possibilities
3. perturbation analysis to make sure the “solution” is not overly sensitive to the optimal setting

I assumed 30bps in transaction costs and slippage in backtesting. Trade profitability is quite high, so is not terribly sensitive to transaction cost. I am expecting < 10bps in transaction costs, so the remaining 20bps relates to execution slippage.

Results

99% of the 1600 stratlets were very positive out-of-sample. The remaining ~15 losing stratlets had easily identified issues during the in-sample period, with low to negative performance in-sample. These 15 portfolios also scored poorly in terms of stationarity as well.

I observed a wide range of risk characteristics across the strategies (Sortino, Calmar, etc), so wanted to understand to what degree the losing trades are correlated across stratlets. If the losses were highly correlated then bundling into a portfolio would not tend to improve the overall risk. Fortunately, as we shall see, the losses are relatively uncorrelated, leading to improved risk characteristics when trading a larger # of stratlets.

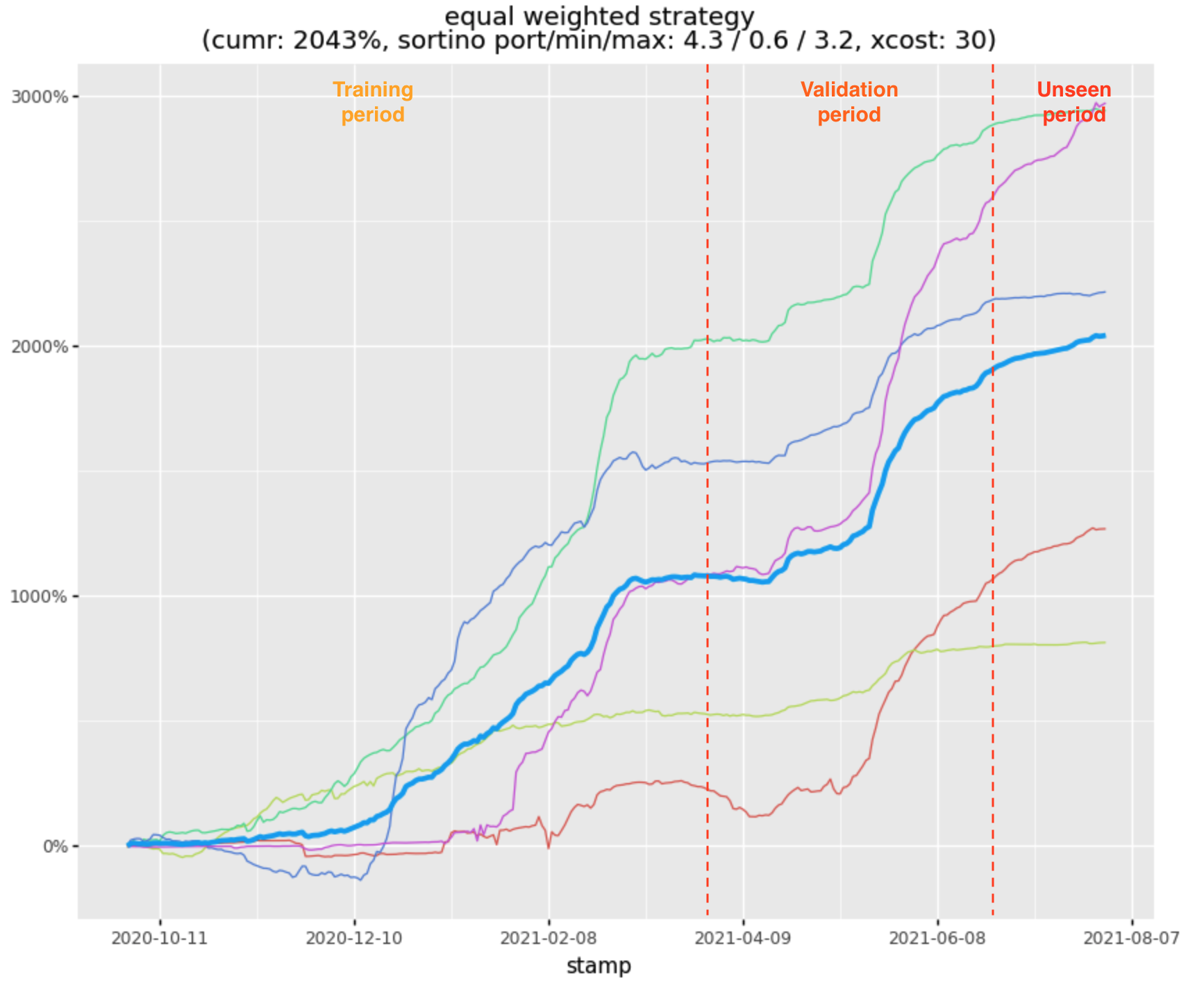
Small Portfolio

Here is the performance of a small portfolio based on higher-liquidity stratlets ranked by the Calmar ratio within the validation period. The individual stratlets have sortino’s ranking from 0.6 to 3.2 within this small set, however the effective Sortino for the portfolio is higher, at 4.3:

Medium Portfolio

The risk characteristics improve even further to 10.3 with the larger top-25 portfolio:

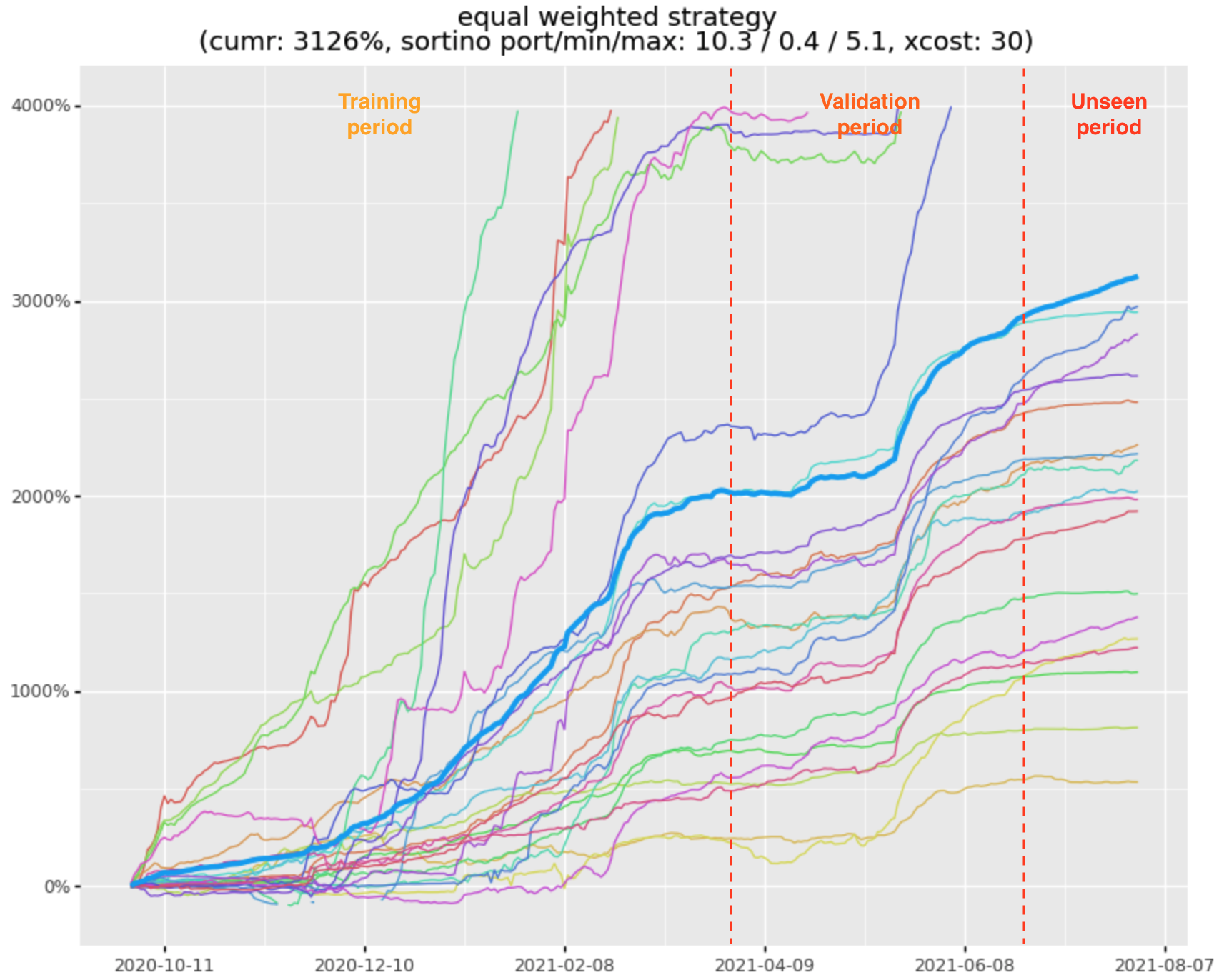
So the good news is that the losses appear to be relatively independent across stratlets allowing us to average these out with other profitable stratlets during the loss periods.

Large Portfolio

I evaluated a portfolio based solely on the sortino seen within the training period, selecting stratlets with sortino > 3. (selecting ~600 stratlets). Note that the validation period was not used in portfolio selection, providing a longer unseen period, from late March to current:

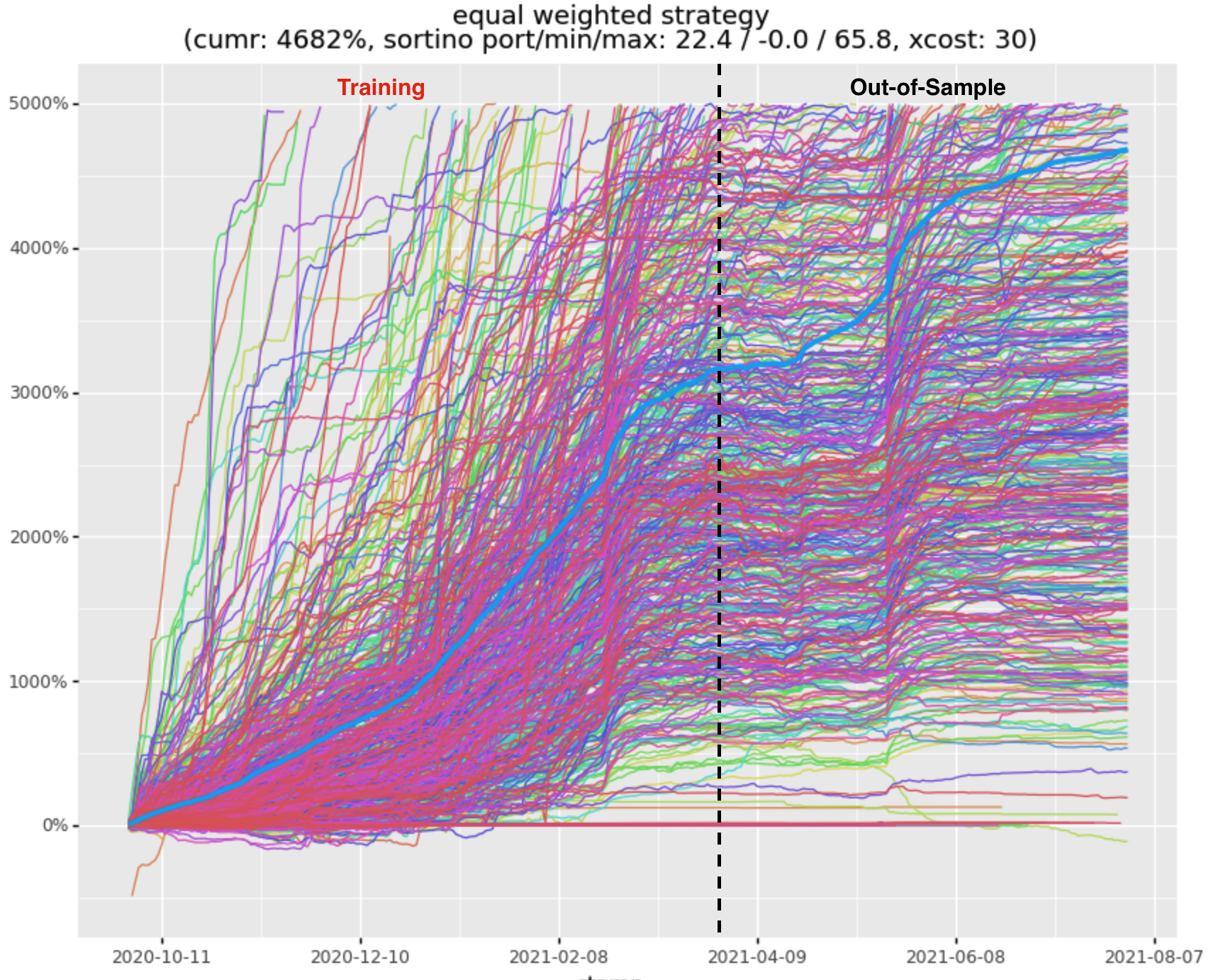
This appears to an excellent result, with a Sortino of 22.4 and 4682% return. However, the return seems too good to be true, and it is. This result assumes we can execute in size (and at equal size) across stratlets. In reality, scaling up this strategy would underweight the majority of stratlets and overweight a smaller set with higher liquidity (the lower liquidity stratlets have higher returns than the highly liquid ones).

Notes

1. I have not accounted for execution failures (for example missed legs)
   • will have to see how this plays out in live
2. Many of these stratlets are liquidity constrained, so the actual return when size adjusted will be lower.
   • the lowest liquidity portfolios can only handle, maybe, 10K / trade, while the highest, potentially a few million.
3. Live performance might degrade by 3 - 5x
   • due to the above considerations
4. The nature of stat/arb is that over time, the market will become more efficient
   • so I expect that the profitability of the strategy will diminish over time.