Arbitrage In DEFI (p1)
I have been building and improving a MEV strategy in DEFI to perform both atomic and non-atomic arbitrage, backrunning, liquidations, etc. In this post will focus on one of the hard algorithmic problems, namely, determining the optimal size and path of arbitrage through swap pools and other protocols.
On Ethereum, for example, there are ~700K ERC20 tokens and a few hundred thousand AMM pools (fortunately only a fraction of these pools and tokens are active). We can consider the possible transactions and interactions across pools as a directed graph, where edges represent flows from a wallet or pool to another pool or wallet. The size of this graph is enormous, perhaps 200K nodes and a similar number of edges. Here is a small example of such a graph:
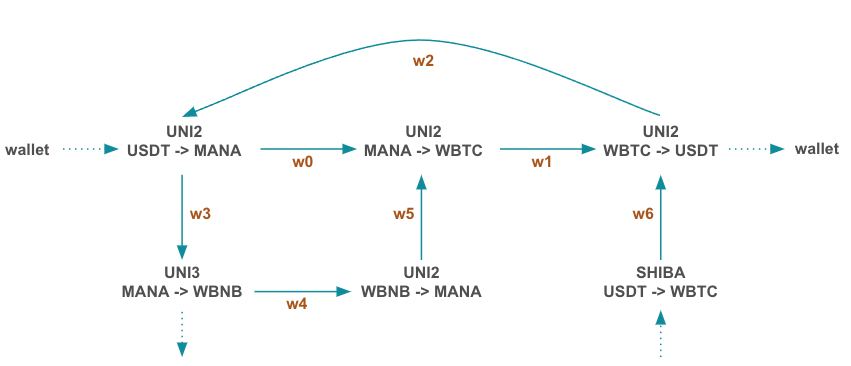
The Problem
Given a source (our wallet) we want to determine if there are profitable arbitrage paths through the graph. Each node represents a swap pool, where the amount-in, in one coin with result in some amount-out in another coin. This presents itself as a max-flow problem, where we want to:
- maximize the net amount out from source -> sink
- i.e. amount into our wallet > amount out of our wallet at the end of the arbitrage paths
- reject arbitrage paths if:
- expected cost of arbitrage > profit or minimum profit target, this includes gas cost & priority fee
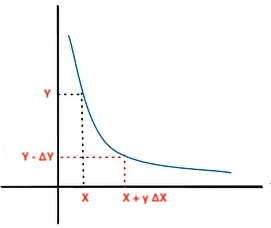
AMMs such as Uniswap V2 (and top of book V3) use the so-called “constant product” formulation for pricing $XY = k$, where X and Y are the reserves of coin 1 and coin 2.
If we want to trade $\Delta X$ for some outgoing amount of coin $\Delta Y$, and assuming $\gamma = (1-fees)$, we arrive at the relation:
\[(X + \gamma \Delta X) (Y - \Delta Y) = k\]expressing the notion that an incoming amount of $\Delta X$ is added to the X reserves and an outgoing amount of $\Delta Y$ is removed from the Y reserves, all the while keeping $k$ constant. Graphically, swapping adjusts size and and price along a hyperbolic curve like this:
We can formulate the problem, the max-flow problem, by determining the weights to assign to edges in the graph. Let us define the weights to be in [0,1], representing the % of coin to flow on a given edge from its immediate source node. Given this setup, the following must be true:
- the sum of weights for outgoing edges must be = 1
- such that all outgoing flow from a node is handled
- a weight on a given edge can be 0
- indeed for a given arbitrage epoch, most weights will be 0 and just the pools and transfers active in the arbitrage will have non-zero weights
So, assuming we know how much size we are starting with at the source, it should just be a matter of determining the weights through the graph such that we end with more size than we started with.
If the pools were linear in terms of input -> output, this is a problem that could be solved with linear algebra, however most AMMs have a non-linear output function. For any given node we could formulate its output based on the weighted incoming flows:
\[\begin{align} amount_{out} (F_i,w_i | i \in edges) &= Y - \frac{k}{X + \gamma \sum_{i \in edges} w_i F_i} \\ \sum_{i \in edges} w_i &= 1 \end{align}\]where \(F_i\) is the flow from the pool associated with the i’th edge and $w_i$ is the weight assigned to an incoming edge. One could create a chain of these equations linking nodes in the graph from source to sink.
Difficulties
The graph of possible trades across pool presents problems:
- all possible traversals of the graph has combinatorial complexity.
- the upper bound is on the order of O(n!), if fully connected
- we encounter cycles
- cycles pose problems for various max-flow or distance problems on a graph; for a max-flow problem we want to have acyclic paths between the source and the sink.
- the amount of flow is non-linear with size, as we have seen above
- in fact Uniswap V2 clones present one of the easier cases for optimisation; Uniswap V3 presents an even more complex discontinuous function from the point of view of optimisation.
The cycle problem
A typical graph of AMM pools will have hundreds of cycles. While we could do a DFS or BFS and eliminate cycles, the DFS expansion would grow astronomically large. Let’s consider a small example:
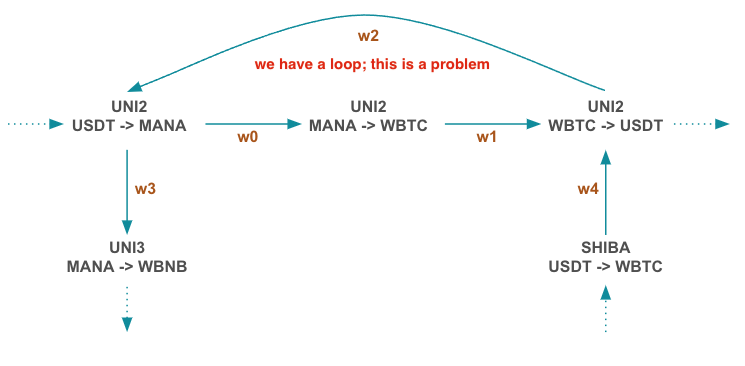
The $w_2$ edge is reasonable if $w_1$ is disconnected ($w_1 = 0$) or vice-versa. We can introduce indicator variables $I_k \in {0,1}$, to gate flow avoiding cycles in the graph:
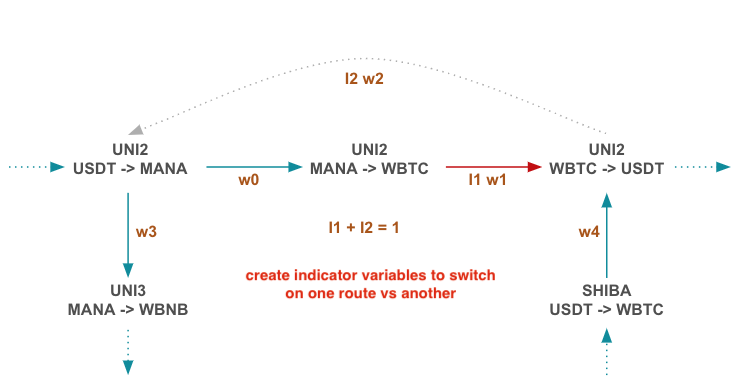
To determine where to put these indicator variables, we can do a breadth-first-search (BFS) from the source down towards the sink and make the following adjustments when a cycle is detected:
- add indicator variable $I_j$ on the outgoing edge completing the cycle
- add indicator variable $I_k$ on incoming edges already visited
- add constraint $I_j + \sum_k I_k = 1$
The above approach eliminates cycles and for proper construction of a max-flow problem.
The optimisation problem
Optimisation is a challenge:
- convex or quasi-convex optimisation
- The bilinear $I_j w_j$ weight-indicator products on edges create non-convex constraints. Unfortunately, this would require Mixed Integer Nonlinear Programming to solve if done with a traditional optimiser. If we get rid of the binary indicator variables we could use a quasi-convex DQCP optimiser.
- We could use a continuous function, albeit with cusp-like derivatives to model an indicator-like variable. This might not be very stable, however.
- size of problem
- The size of the jacobian and other matrices used would be massive, making solving such a system in this way impractical, even without the integer constraints.
- there are other approaches that we will discuss that evade this issue.
- there are also techniques we can use to dramatically reduce the size of the problem
We will discuss and evaluate these in further posts.
Upcoming
We will evaluate the following in coming posts:
- heuristic optimisation
- convergence in DQCP with some reformulation of the problem
- reduction of the problem (by a couple orders of magnitude)